0
-
An empty cart
You have no item in your shopping cart
The critical factor in the creation and maintenance of dust-laden air or particle contaminated water is the nature of the particle, in terms of its size and its relative density. This is because of the development of a constant, terminal velocity by a particle falling freely through a fluid, whose value, as demonstrated by Stokes ‘ law, is:
● directly proportional to the square of the particle diameter
● directly proportional to the difference between particle and fluid densities
● indirectly proportional to fluid viscosity.
This relationship is strictly true only for spherical particles falling while isolated from one another by some distance. Non-spherical particles are accounted for by the use of an effective diameter (often determined by the reverse process of measuring a terminal velocity and calculating back to the diameter). Stokes’ law holds well enough in the case of fluids with a low solids concentration such as concerns a study of contaminant removal.
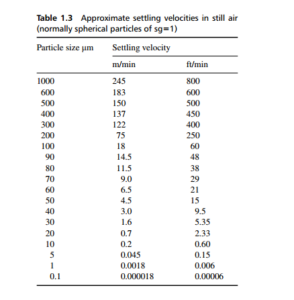
If the particle size is small enough so that the terminal velocity is very low, or if there are random movements in the fluid at velocities in excess of this terminal figure, then the particle effectively does not settle out, and a stable suspension results – which may then need decontaminating. The settling velocity in air of a spherical particle, whose specific gravity is 1, is given by:

where d is the particle diameter, expressed in um. An array of values for terminal settling velocities in air for a spherical particle with sg = 1 is given in Table 1.3.